Leetcode 总结 - 排序
Overview
排序算法
1. swap算法
- 常规SWAP,使用额外变量
- 加减法(需要判断A B不一样)
1A = A + B;
2B = A - B;
3A = A - B;
- bit异或操作(需要判断A B不一样)
1A = A ^ B;
2B = A ^ B;
3A = A ^ B;
2. 冒泡排序
稳定性:稳定
提前结束+ 优化
1public int[] bubbleSort(int[] arr) {
2 if (arr.length < 2) return arr;
3 boolean swapped = true;
4 int lastSwappedIdx = arr.length - 1 ;
5 int swappedIdx = -1;
6 // lastSwappedIdx表示前一轮交换的最终位置,即下标为lastSwappedIdx是未排序部分中的最后一个数的下标,
7 // 因此for中的界是i < lastSwappedIdx而不需要写成i <= lastSwappedIdx
8 while (swapped) { // 当swapped = false时,排序完成
9 // 本轮执行是否有交换的标志,若无则true,若有则false
10 swapped = false;
11 // 每轮循环,通过依次向右比较两个数,将本轮循环中最大的数放到最右
12 for (int i = 0; i < lastSwappedIdx; i++) {
13 // 若左大于右则交换,并将swapped置为true
14 if (arr[i] > arr[i + 1]) {
15 swap(arr, i, i + 1);
16 swapped = true;
17 swappedIdx = i;
18 }
19 }
20 lastSwappedIdx = swappedIdx;
21 }
22 return arr;
23}
3. 选择排序
稳定性:不稳定
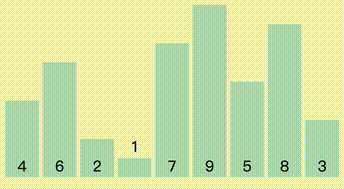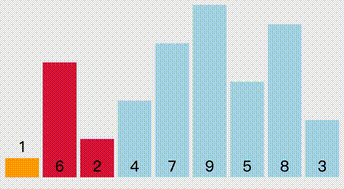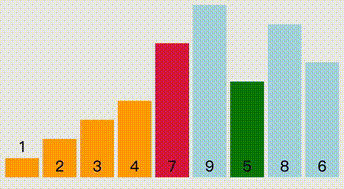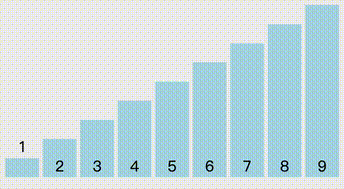
算法说明:
- 第0次:设置最终交换的a为第0个,计做num[0],然后往后找,找到小于num[0]的,更新index,即num[index],直到结束,然后交换index 和第0号元素
- 第N次:最终交换index 和N号元素
普通版本
1public int[] selectSort(int[] arr) {
2 if (arr.length < 2) return arr;
3 // n - 1 轮次执行,当前 n - 1 个元素排好后,最后一个元素无需执行,故 i < arr.length - 1
4 for (int i = 0; i < arr.length - 1; i++) {
5 int minIdx = i;
6 // 找到本轮执行中最小的元素,将最小值下标赋值给min
7 for (int j = i + 1; j < arr.length; j++) {
8 if (arr[j] < arr[minIdx]) minIdx = j;
9 }
10 // 若本轮第一个数字不是最小值,则交换位置
11 if (minIdx != i) swap(arr, i, minIdx);
12 }
13 return arr;
14}
双元选择排序
选出每次两个
1public int[] selectSortDouble(int[] arr) {
2 if (arr.length < 2) return arr;
3 int n = arr.length;
4 // 每轮确定两个数字,因此界也会动态变化
5 for (int i = 0; i < n - 1 - i; i++) {
6 int minIdx = i, maxIdx = i;
7 // 找到本轮执行中最小和最大的元素
8 for (int j = i + 1; j < n - i; j++) {
9 if (arr[j] < arr[minIdx]) minIdx = j;
10 if(arr[j] > arr[maxIdx]) maxIdx = j;
11 }
12 // 若本轮最大值等于最小值,说明未排序部分所有元素相等,无需再排序
13 if(minIdx == maxIdx) break;
14 // 若本轮第一个数字不是最小值,则交换位置(将最小值与本轮第一个数字交换位置)
15 if (minIdx != i) swap(arr, i, minIdx);
16 // 在交换i和minIdx时,有可能出现i即maxIdx的情况,此时需要修改maxIdx为minIdx
17 if(maxIdx == i) maxIdx = minIdx;
18 // 若本轮最后一个数字不是最大值,则交换位置(将最大值与本轮最后一个数字交换位置)
19 if (maxIdx != n - 1 - i) swap(arr, n - 1 - i, maxIdx);
20 }
21 return arr;
22}